Area Of A Circle Formula Using Circumference

The circle is a two-dimensional shape, which possesses its area and perimeter. The perimeter of the circle is also termed as the circumference, which is the measure around the circle. The area of the circle is the region defined by it in a 2D plane. A circle is also termed as the locus of the points drawn at equidistant levels from the centre. The measure from the centre of the circle to the outer line is its radius.

Diameter is the line that separates the circle into two equal parts and is also equal to twice the radius. A circle is a fundamental shape that is measured in terms of its radius. In geometry or mathematics, a circle can be defined as a special variety of ellipse in which the eccentricity is zero and the two foci are coincident. As with triangles and rectangles, we can attempt to derive formulas for the area and "perimeter" of a circle.

Calculating the circumference of a circle is not as easy as calculating the perimeter of a rectangle or triangle, however. Given an object in real life having the shape of a circle, one approach might be to wrap a string exactly once around the object and then straighten the string and measure its length. This first argument is an example of MP7, Look For and Make Use of Structure. The key to this argument is identifying that all circles are similar and then applying the meaning of similarity to the circumference. The second argument exemplifies MP8, Look For and Express Regularity in Repeated Reasoning. Here the key is to compare the circle to a more familiar shape, the triangle.

The circumference of a circle of radius $r$ is $2\pi r$. This well known formula is taken up here from the point of view of similarity. It is important to note in this task that the definition of $\pi$ already involves the circumference of a circle, a particular circle.

In order to show that the ratio of circumference to diameter does not depend on the size of the circle, a similarity argument is required. Two different approaches are provided, one using the fact that all circles are similar and a second using similar triangles. This former approach is simpler but the latter has the advantage of leading into an argument for calculating the area of a circle. The first solution requires a general understanding of similarity of shapes while the second requires knowledge of similarity specific to triangles. The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae.

In above program, we first take radius of circle as input from user and store it in variable radius. Then we calculate the circumference of circle using above mentioned formulae and print it on screen using cout. I am going to discuss these axioms in a moment, but first let me show how Claim follows. But by Axiom 1 the length of the arc $PBQ$ is greater than $PQ$, while it follows from Euclid III.2 that $OB$ is greater than $OA$. Applying symmetry, this implies Claim in this case, and ought to suggest how the reasoning goes in general. A circle is a closed curve formed by a set of points on a plane that are the same distance from its center.

The area of a circle is the region enclosed by the circle. The area of a circle is equals to pi (π) multiplied by its radius squared. The radius, the diameter, and the circumference are the three defining aspects of every circle.

Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle. You can also think of the radius as the distance between the center of the circle and its edge. Like all geometric shapes, circles take up space and a formula is required to calculate the area.

If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. The properties of circles have been studied for over 2,000[/latex] years. All circles have exactly the same shape, but their sizes are affected by the length of the radius, a line segment from the center to any point on the circle. A line segment that passes through a circle's center connecting two points on the circle is called a diameter. A circle is a closed shape formed by tracing a point that moves in a plane such that its distance from a given point is constant.

The word circle is derived from the Greek word kirkos, meaning hoop or ring. In this article, we cover the important terms related to circles, their properties, and various circle formulas. From point B, on the circle, draw another circle with center at B, and radius OB.

The intersections of the two circles at A and E form equilateral triangles AOB and EOB, since they are composed of 3 congruent radii. Extend the radii forming these triangles through circle O to form the inscribed regular hexagon with 6 equilateral triangles. Is called the circumference and is the linear distance around the edge of a circle. The circumference of a circle is proportional to its diameter, d, and its radius, r, and relates to the famous mathematical constant, pi (π).

A circle is known as a closed plane geometrical shape. Technically, it is the locus of a point that moves around a fixed point at a fixed distance that is away from that point. A circle is basically a closed curve that has its outer line at an equal distance from the centre. This fixed distance from the central point is known as the radius of the circle. In our day to day life, we often see many examples like a pizza, wheel, etc. Let us learn about these terms in regards to a circle.

We use this formula to measure the space which is occupied by either a circular plot or a field. In this article today, we will discuss the area of circle definition, the area of a circle equation, its circumference and surface area in detail. Cover the circle with concentric circles of "r" radius. After dividing the circle along the designated line shown in the above figure and spreading the lines, the outcome will be a triangle. The base of the triangle will be equivalent to the circumference of the circle, and its height will be identical to the radius of the circle. Below is the formula calculation for the same.

The distance from the centre to the outer line of the circle is called a radius. It is the most important quantity of the circle based on which formulas for the area and circumference of the circle are derived. Twice the radius of a circle is called the diameter of the circle. The diameter cuts the circle into two equal parts, which is called a semi-circle. When we use the formula to calculate the circumference of the circle, then the radius of the circle is taken into account.

Hence, we need to know the value of the radius or the diameter to evaluate the perimeter of the circle. When we have the length of the diameter or the radius or the circumference of the circle, we can find the surface area of the circle by using the surface area formula. This surface area of the circle is represented in terms of square units. Is made up of a large number of concentric circular pieces of very thin string. The first step is to approximate the area of a circle using a regular polygon.

We inscribe a regular polygon in the circle and split up the polygon into congruent isosceles triangles as shown below. The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius. A circle is the set of points in a plane that are equidistant from a given point . The distance from the centeris called the radius, and the point is called the center.

The angle a circle subtends from its center is a full angle, equal to or radians. The proof of this theorem in the extant version immediately follows its statement. I'll sketch it below, with a bit of explanation and a few more figures added. The basic idea is almost exactly the same as that of Euclid's proof of Theorem XII.2, which asserts that the area of a circle is proportional to the square of its radius.

The overlap of Archimedes' argument with that of Euclid should not be surprising, since Euclid's Theorem XII.2 is an immediate consequence of Archimedes'. The sectors are pulled out of the circle and are arranged as shown in the middle diagram. The length across the top is half of the circumference. When placed in these positions, the sectors form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble a parallelogram.

As seen in the last diagram, the parallelogram ca be changed into a rectangle by slicing half of the last sector and placing it to the far left. Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

Finding the radius is not always easy, especially if you don't have the circle's center. You can calculate the area using the diameter instead. The same formula applies as above, but you need first to calculate the radius of the circle. Simply divide the diameter by 2 to get the radius. The circle circumference is the perimeter of an elliptical or circular shape. In other words, this is the arc length or boundary length of the circle; if we straightened it out or open up in a line segment.

In this method, we divide the circle into 16 equal sectors. The sectors are arranged in such a way that they form a rectangle. All sectors are similar in area, so hence all sectors' arc length would be equal.

The circle's area would be the same as the area of the parallelogram shape or rectangle. Only a mathematician can genuinely understand the practical importance of formulas for calculating area, radius, diameter, or circle circumference. While most people think that formulas have no practical use, they are critical factors in many everyday life routines.

The perimeter of a closed figure is known to be the length of its total boundary. When it comes to the circles, the perimeter is called by a different name. It is referred to as the 'circumference' of the given circle. This circumference is known as the total length of the boundary of the given circle. If we open the circle and form a straight line, the length of the straight line that we get is the circumference. For defining the circumference of a circle, we need to know a term called 'pi'.

Consider the circle shown below having its centre at O and radius r. Remember that circumference and perimeter are alway measured in feet, inches, centimeters, etc. Area is alway measured in square units and volume always in cube units. To recall, the area is the region that occupied the shape in a two-dimensional plane.

In this article, you will learn the area of a circle and the formulas for calculating the area of a circle. Knowledge of area and perimeter of squares, rectangles, triangles and composite figures. Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye. While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel? Since area is a measure of two dimensions, you always report area in square units like square inches or square feet .

This is especially important when calculating the area of a circle for an assignment since an answer without correctly reported units is likely incorrect or incomplete. Pi (π) is a non-algebraic number that represents the ratio of the distance around the circle to its diameter, usually estimated as 3.14. To solve for area, square the radius then multiply by 3.14. And as Math Open Reference states, the formula takes the circumference of the entire circle (2πr).

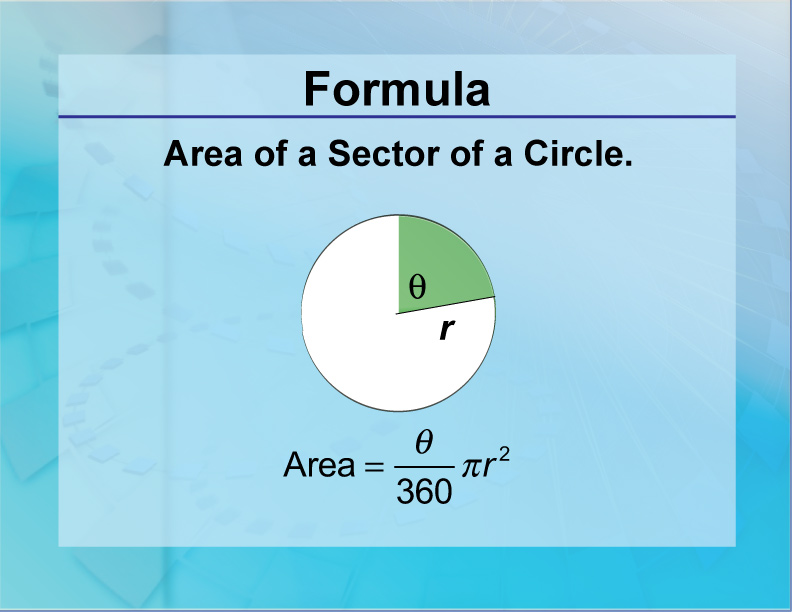
It reduces it by the ratio of the degree measure of the arc angle to the degree measure of the entire circle . In this formula, r represents the radius, which is a segment that connects the center of the circle to a point on the edge of the circle. It is half the size of the diameter, and every radius inside of a circle will be the same. Let's take a brief look at how to find the area of circles. Π shows the ratio of the perimeter of a circle to the diameter. Therefore, when you divide the circumference by the diameter for any circle, you obtain a value close enough to π.

This relationship can be explained by the formula mentioned below. The following are some mathematical formulae that will help you calculate the area and perimeter/circumference of a circle. You can refer to the below screenshot to see the output for the python program to calculate the area and perimeter of a circle using class.

You can refer to the below screenshot to see the output for the python program to calculate the area and circumference of a circle using an inbuilt math module. Here, we will see python program to calculate the area and circumference of a circle using an inbuilt math module. Archimedes' argument has the same basic design as other arguments applying the method of exhaustion - carrying out some potentially infinite process until something happened to stop it. Eudoxus is elsewhere said to be the one who invented the extremely sophisticated way in which Euclid proved results about possibly irrational ratios.

The method of exhaustion and the theory of ratios are the two most subtle parts of ancient Greek mathematics. They provided the touchstone of rigor in mathematics for several centuries, but applying them was an awkward business because it generally required a different approach to each problem. Still, there was no alternative until Cauchy in the early nineteenth century began the development of modern mathematical reasoning by introducing his algebra of inequalities. It involves dividing the circle into many sectors and rearranging the sectors to form a rectangle. The base of the rectangle is shown to be πr and the height of the rectangle is r. The area of the rectangle is then the product of πr and r.